|
This post is completed by 3 users
|
Add to List |
48. Determining Whether a Given Binary Tree is a Binary Search Tree (BST)
Objective: Given a Binary tree, find out whether it's a binary search tree or not.
Approach:
Method 1: If the tree doesn't have duplicates
- Do the inorder traversal of the given binary tree.
- check if the previously visited node is less than the current node value.
- If yes, then return true
- Else return false.
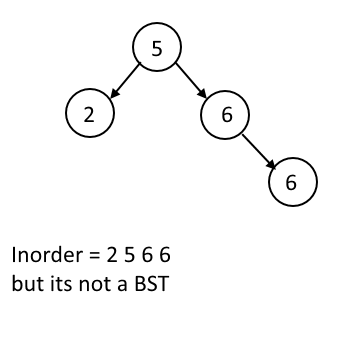
The above method works only when the tree doesn't have any duplicates. (we can choose that either duplicate will either go to the left OR on the right but we cannot choose it randomly while constructing the tree, we need to decide before we construct the tree and it has to be consistent throughout and here we are deciding that duplicates should go to the left subtree.) see figure,
Method 2: The Max/Min Solution :
When we talk about binary search trees we talk about one property i.e. leftChild.data <=root.data<rightChild, but checking this property alone at every node is not gonna work out, why?, see this example
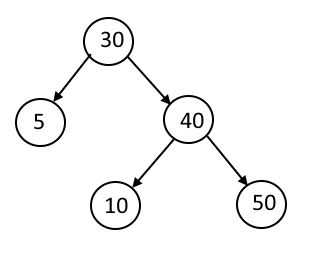
Now in the above example, you can see that when you validate Node 40, 10<=40<50 it will return true and when you validate Node 30, 5<=30<40, it will return true but as you can see this tree is not BST since 10 is smaller than 30 so it should be on the left of the 30. Actually, all the nodes less than 30 should be on the left and all the nodes greater than 30 should be on the right.
How would you achieve that???
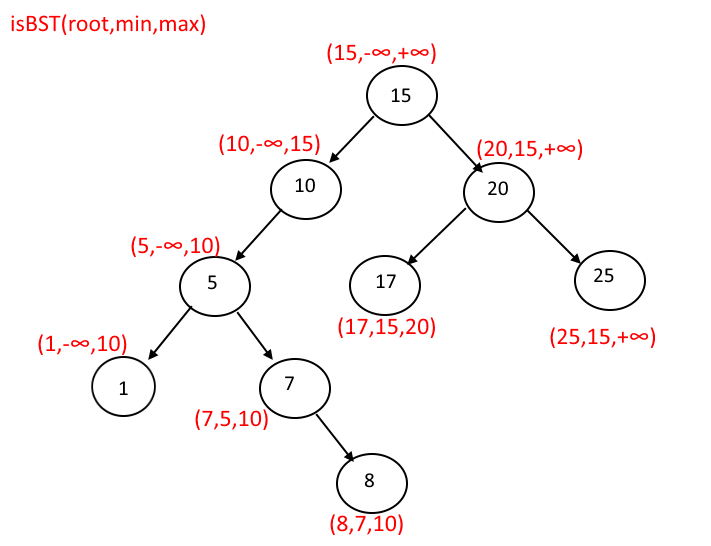
The root value can have any value between -∞ to + ∞. When you validate the right child of 30, it can take any value between 30 and + ∞. When you validate the left child of 30, it can take any value between - ∞ and 30. likewise, when you validate the left child of 40, it can take any value between 30 and 40.
So the idea is to Pass the minimum and maximum values between which the node's value must lie.
we start with the range minimum = Integer.MIN_VALUE and maximum = Integer.MAX_VALUE, so when checking the left node of 30(root), the minimum will be = Integer.MIN_VALUE and maximum = 30, and so on. See the figure for the better understanding.
Complete Code for Both the methods:
Output :
Tree is 5 10 15 20 25 30 35 is Tree BST ?? METHOD 1 : true is Tree BST ?? METHOD 2 : true Tree is 5 10 15 40 20 25 30 35 is Tree BST ?? METHOD 1 : false is Tree BST ?? METHOD 2 : false

