|
Be the first user to complete this post
|
Add to List |
279. Disjoint Set | Union-Find Algorithm - Union by rank and path compression
Earlier we have seen the complete implementation of Disjoint Set. We strongly recommend reading this before continue.
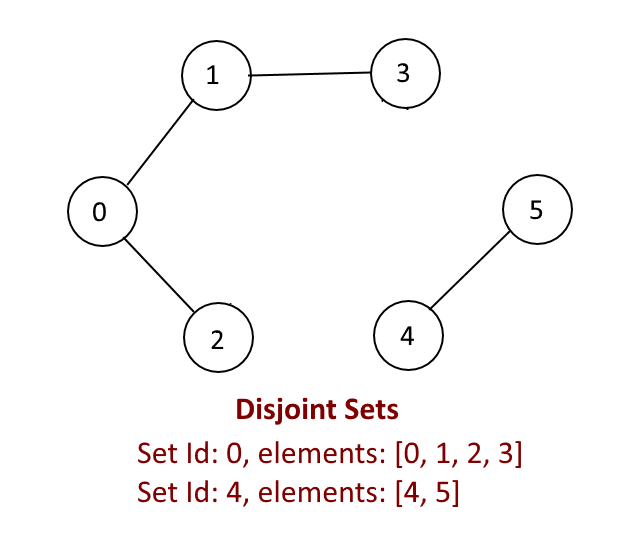
Disjoint Set operations –
- MakeSet(x)
- Find(x)
- Union(x,y)
Click here to read about these operations in detail.
How Disjoint Set is optimized:
- Union by rank.
- Path by compression.
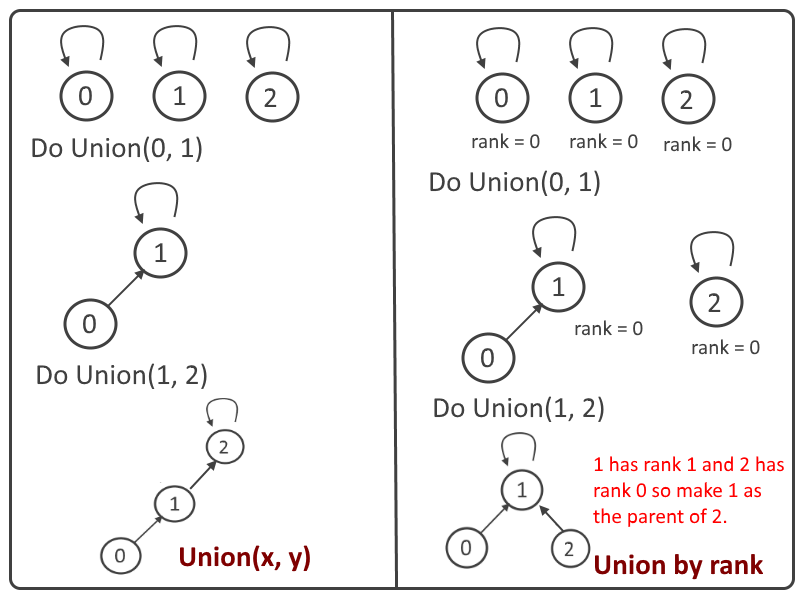
Union by rank:
Uses Find to determine the roots of the trees x and y belong to. If the roots are distinct, the trees are combined by attaching the root of one to the root of the other. If this is done naively, such as by always making x a child of y, the height of the trees can grow as O(n). We can optimize it by using union by rank.
Union by rank always attaches the shorter tree to the root of the taller tree.
To implement union by rank, each element is associated with a rank. Initially a set has one element and a rank of zero.
If we union two sets and
- Both trees have the same rank - the resulting set's rank is one larger
- Both trees have the different ranks - the resulting set's rank is the larger of the two. Ranks are used instead of height or depth because path compression will change the trees' heights over time.
Worst case complexity: O(LogN)
Explanation:
Pseudo Code:
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
// x and y are already in the same set
if xRoot == yRoot
return
// x and y are not in same set, so we merge them
if xRoot.rank < yRoot.rank
xRoot.parent := yRoot
else if xRoot.rank > yRoot.rank
yRoot.parent := xRoot
else
xRoot.parent := yRoot
yRoot.rank := yRoot.rank + 1
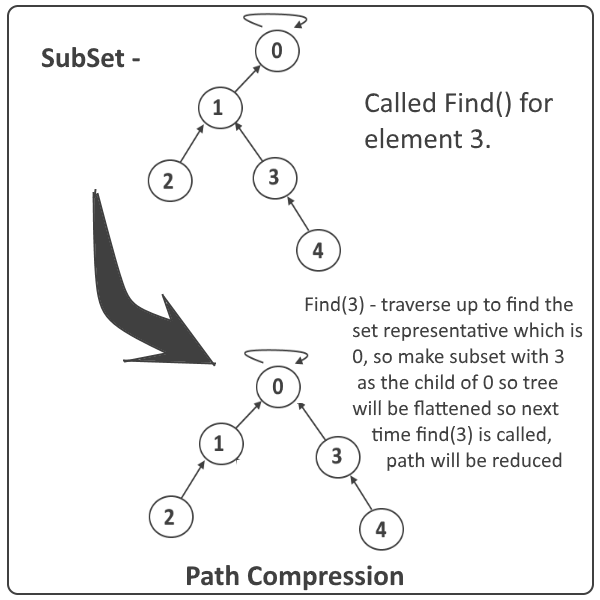
Path compression:
Path compression` is a way of flattening the structure of the tree whenever Find is used on it. Since each element visited on the way to a root is part of the same set, all of these visited elements can be reattached directly to the root. The resulting tree is much flatter, speeding up future operations not only on these elements, but also on those referencing them.
Explanation:
Pseudo code:
function Find(x)
if x.parent != x
x.parent := Find(x.parent)
return x.parent
MakeSet
The MakeSet operation makes a new set by creating a new element with a unique id, a rank of 0, and a parent pointer to itself. The parent pointer to itself indicates that the element is the representative member of its own set.
The MakeSet operation has O(1) time complexity.
Pseudo code:
function MakeSet(x)
if x is not already present:
add x to the disjoint-set tree
x.parent := x
x.rank := 0
Output:
Disjoint Sets: Set Id: 0 elements: [0, 1, 2, 3] Set Id: 4 elements: [4, 5]
Ref: wiki

