This post is completed by 1 user

  • 0
 Add to List
Hard

368. Max Flow Problem - Ford-Fulkerson Algorithm

Objective: Given a directed graph that represents a flow network involving source(S) vertex and Sink (T) vertex.  Each edge in the graph has an individual capacity which is the maximum flow that edge allows.

Flow in the network has the following restrictions-

  • Input flow must match to output flow for each node in the graph, except the source and sink node.
  • Flow out from source node must match with the flow in to sink node.
  • Flow from each edge should not exceed the capacity of that node.

Write an algorithm to find the maximum flow possible from source (S) vertex to sink (T) vertex.

Example:

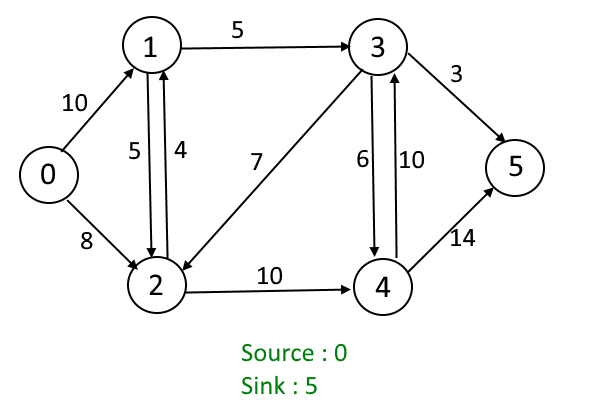
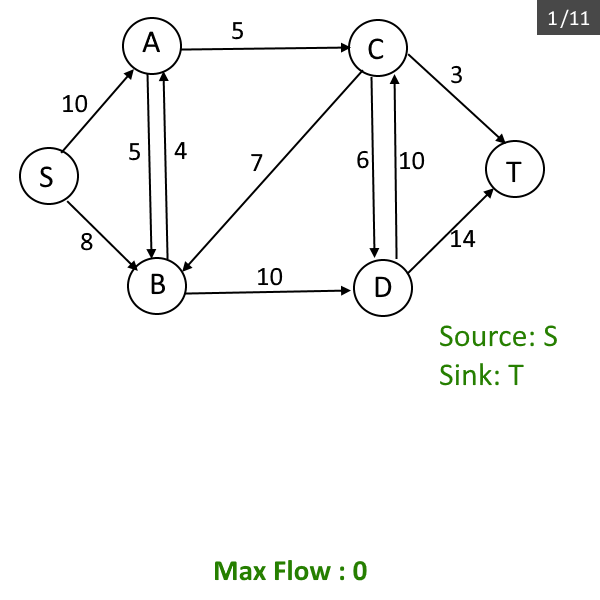
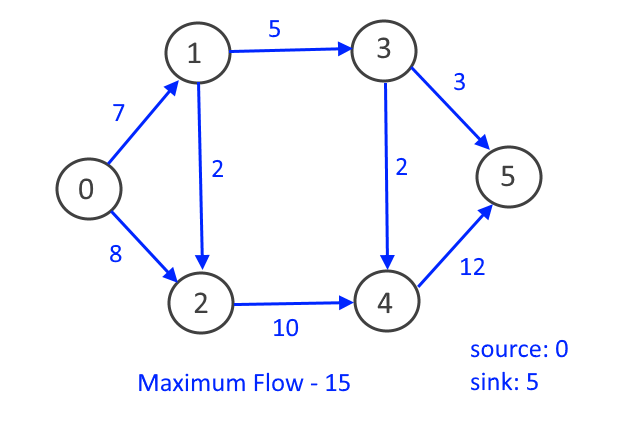
Given the graph, each edge has a capacity (the maximum unit can be transferred between two vertices). Find out the maximum flow which can be transferred from source vertex (S) to sink vertex (T).

We strongly recommend reading the following article before continue reading

  1. Max Flow problem – Introduction
  2. Graph – Breadth-First Search

Ford-Fulkerson Algorithm:

In simple terms, Ford-Fulkerson Algorithm is: As long as there is a path from source(S) node to sink(T) node with available capacity on all the edges in the path, send the possible flow from that path and find another path and so on. Path with available capacity is called the augmenting path.

Pseudo Code:

Inputs Given a Network G = (V, E) with flow capacity c, a source node s, and a sink node t

Output: Compute a flow f from s to t.

  1. Initialize max_flow←0
  2. Initialize f(u,v)← cf (u, v)  for edges (u, v).
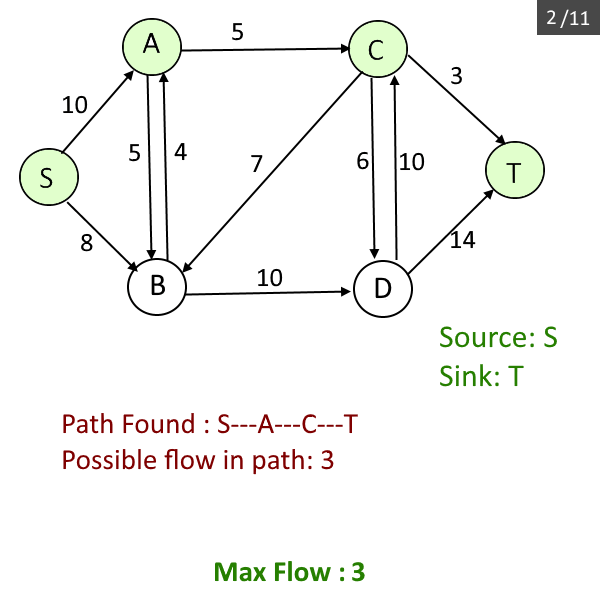
  3. While there is a path p from s to t in Gf (residual graph), such that flow capacity, cf (u, v) > 0 for all the edges (u, v) in path p
    • Find cf(p) = min{cf(u, v): (u, v) ∈ p } (flow possible in path p. pick the minimum capacity among all edges).
    • Add max_flow = max_flow + cf(p)
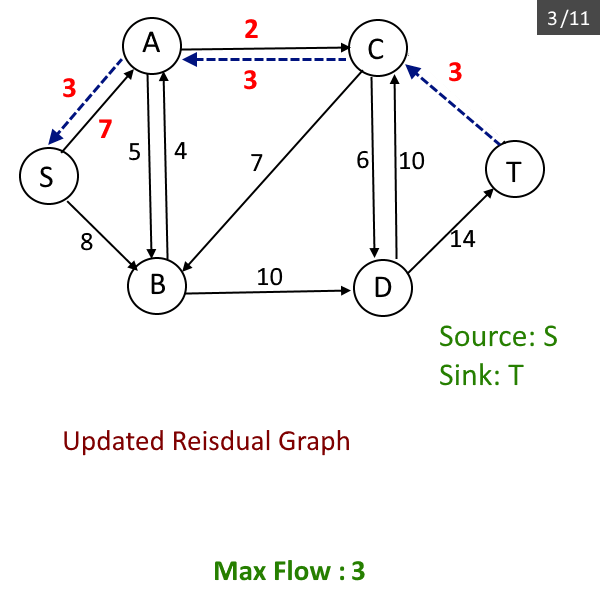
    • For each edge (u, v) in path p
      • f(u, v) ← f(u, v) - cf(p) (reduce the capacity of each edge in path)
      • f(v, u) ←f(v, u) + cf(p) (The flow will returned by back edge, might get used later).
  4. Return max_flow.

Let's understand the above pseudo-code in detail

  1. Initialize max_flow  = 0 (this will be the final answer) and initialize flow for each edge in the graph as the capacity of that edge.
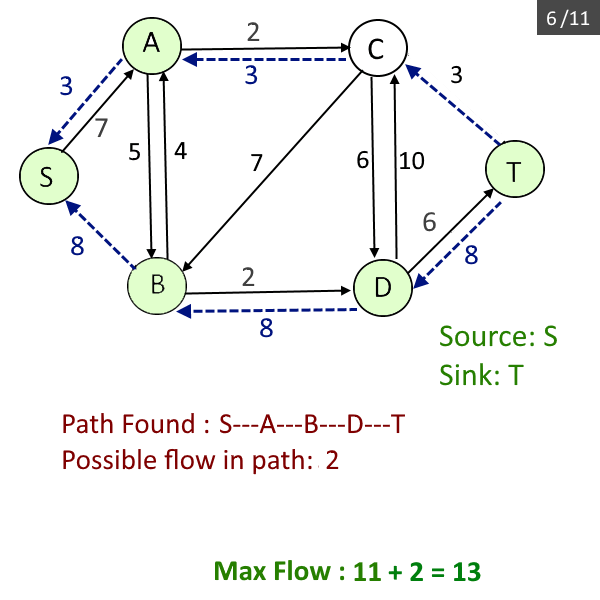
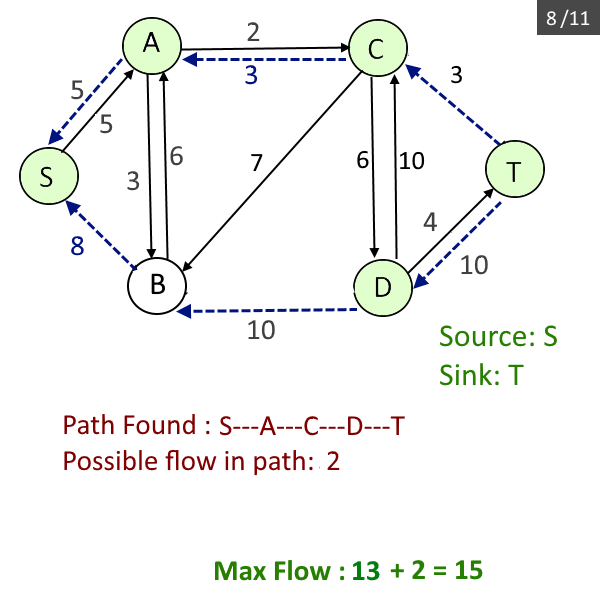
  2. Find the path(p) from source s to sink t wherein each edge in the path has capacity > 0. Do the Breadth-first search to find the path.
  3. Find the maximum flow possible among that path found (it be the minimum capacity among all edges in the path) in the previous step and add it to the max_flow.
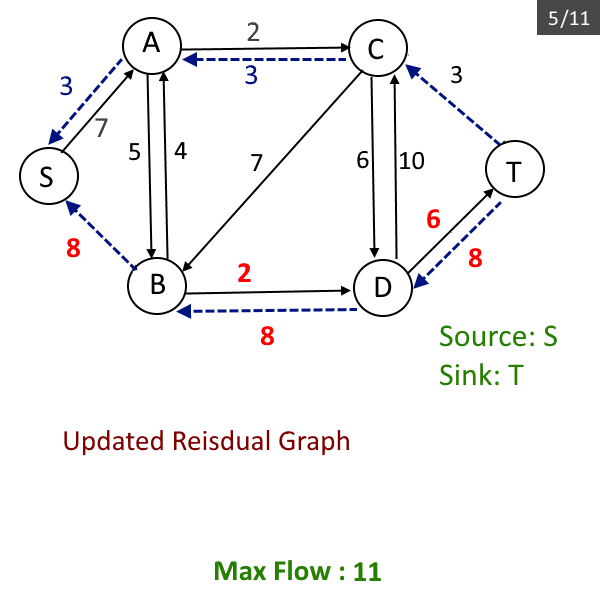
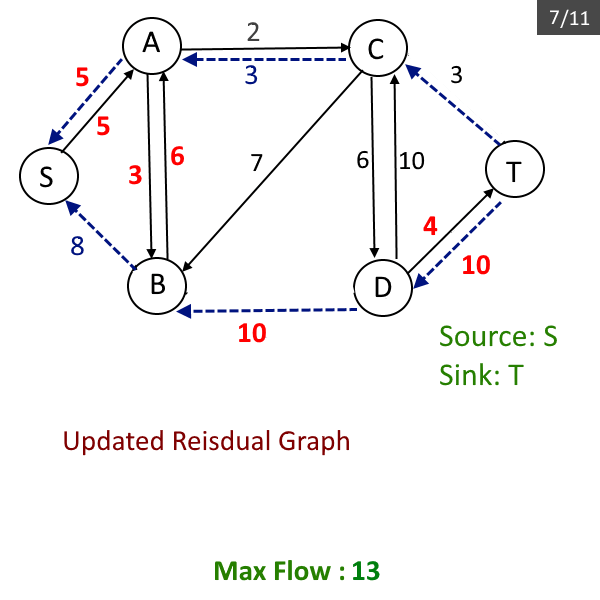
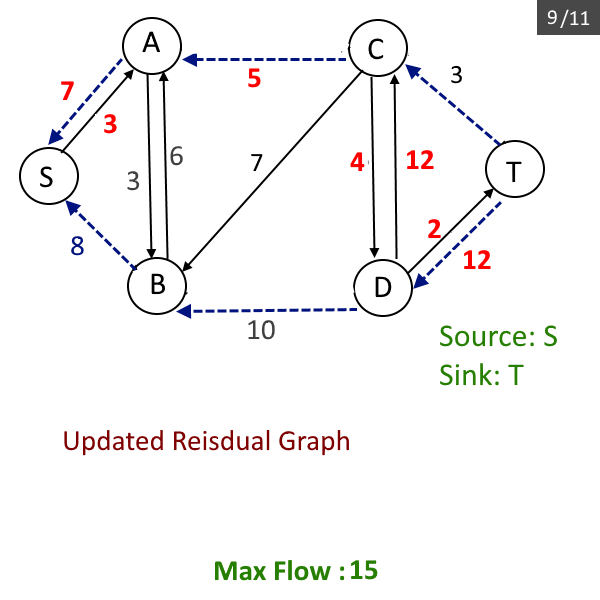
  4. Update the residual graph, reduce each edge capacity by flow possible in the previous step and add the flow in the reverse edge, add the reverse edge if needed (Please read this if you don't know about residual graph).
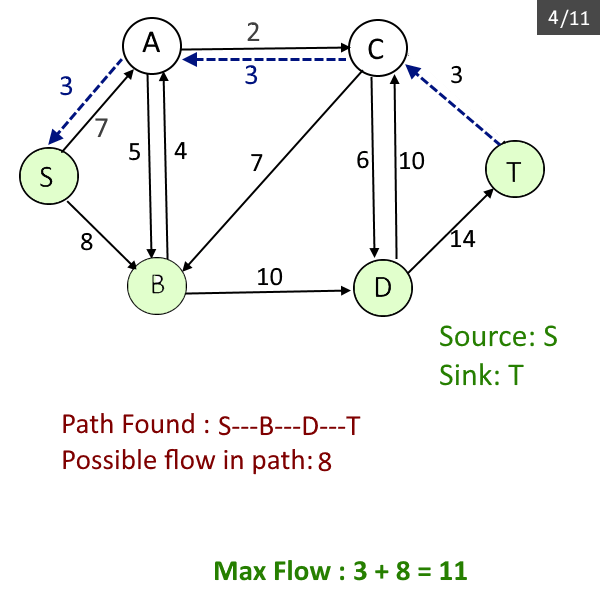
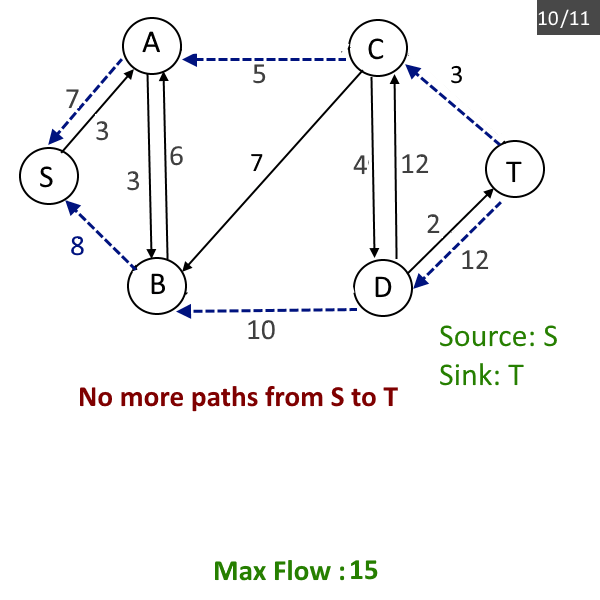
  5. Repeat the steps from b to d till there is a path from source to sink.
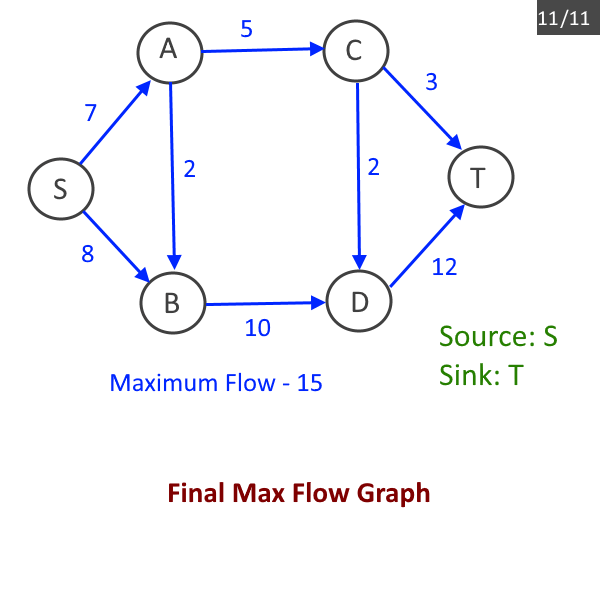
  6. Return max_flow.

Output:

Maximum flow from source: 0 to destination: 5 is: 15

Notes:

  • Ford-Fulkerson algorithm is also called the Ford-Fulkerson method.
  • It is called method instead of the algorithm since the approach to find the augmenting path in the residual graph has many implementations with different run times.
  • It is a greedy algorithm.
  • Ford–Fulkerson is often also used for the Edmonds–Karp algorithm, which is a fully defined implementation of the Ford–Fulkerson method.

Related Problems: